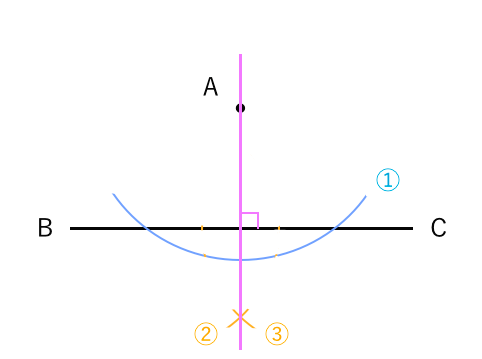
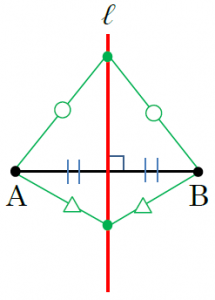
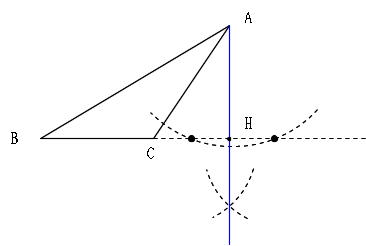
る。三平方の定理は,中学校での最重要学習内容 の1つであるので,これを学力検査で毎年出題し ているのは当然といえる。三平方の定理が複数題 出題されることが多い。また,証明問題は毎年出 題されているが,内容は三角形の相似や角度の相 他の垂線の作図方法を参考にするやり方を考えてみましょう。 直線上にない点を通る垂線のうち、1つ目の方法は、次のような手順で作図するのでした。 直線 $\ell$ 上に2点をとり、それらを中心として点 P を通る円をかく、そして交点を結ぶ。こういうやり(4)四角形の向かい合う辺を(④)という。 (5)4つの辺が等しい四角形を(⑤)という。 ①② ③④ ⑤ 2次のことばの定義を書きなさい。知識理解(2点×2) ①平行四辺形 ②二等辺三角形 3次の図で, χ,yの値を求めなさい。
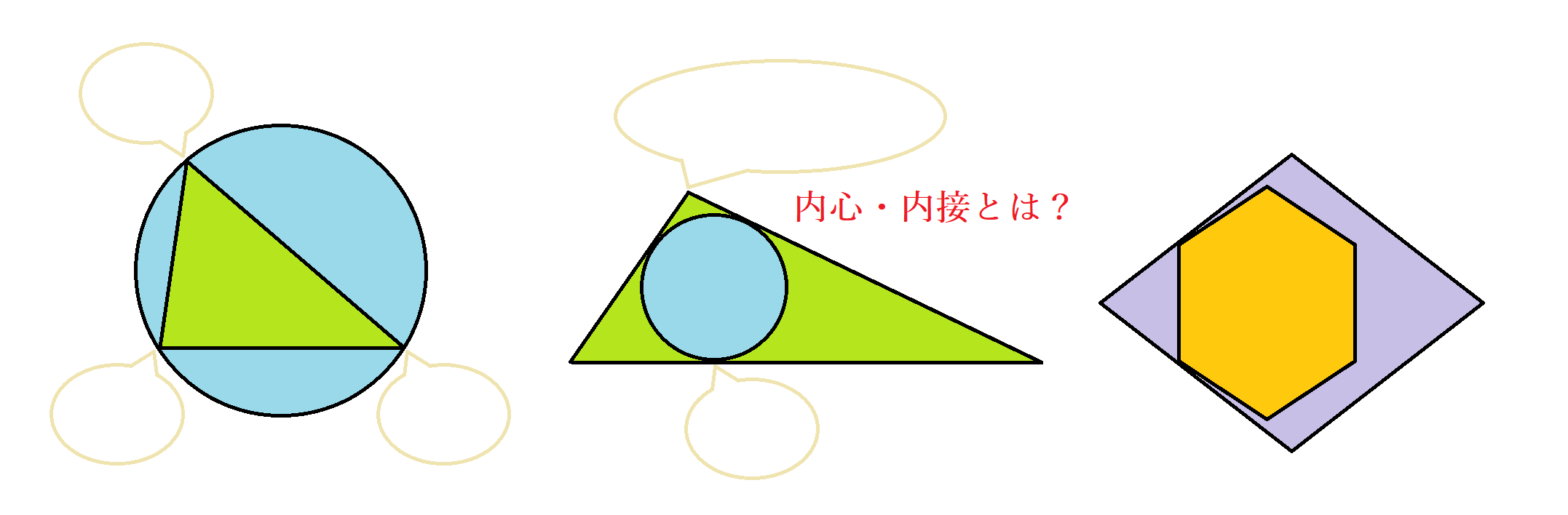
数学 三角形の内心とは 角の二等分線の作図を踏まえた内接円の書き方と証明 Curlpingの幸せblog
三角形 垂線 書き方
三角形 垂線 書き方- 五心とは、三角形の 頂点や辺に関連する特徴的な \bf {5} つの点 のことです。 「重心」「内心」「外心」「垂心」「傍心」の 5 つがあります。 名前に「心」とついている通り、それぞれあるものの中心になっています。 重心 重さの中心 ( 1 点で全体を 三平方の定理で直角三角形の辺の長さを計算してみると、 x² = 3² 5² x = √34 になるね。 答えが整数じゃなくてスッキリしないけど、こういう答えもありだ。 Step3 ピタゴラスが悩んだ直角二等辺三角形 つぎは、 直角二等辺三角形の辺の長さ を三平方



簡単にわかる 垂線を作図する方法 苦手な数学を簡単に
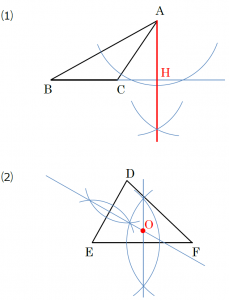
問下図のように頂点の1つが原点Oにあり、他の2頂点が、A(a 1 ,a 2 )とB(b 1 ,b 2 )である三角形OABの点Bから辺OAに下した垂線の足Hの座標を求めよ。 解答1 先ず、点Bを通り線分OAに垂直な直線の方程式2を作る。 (上図に、その直 三角形の各頂点から対辺に垂線をひきます。 垂線は3本できますが、この3本の線は1点で交わります。 この点を、この三角形の 垂心 (orthocenter) といいます。 ただ、「3本の垂線が1点で交わる」ことは、自明なことではありません。垂線の足の を表示するため、垂線の左右に 充分な長さが取れるよう制約条件の調整を考える 三角形の頂点の値を($2,$3)とする \qbezier($2,$3)($2,$4)($2,0) ←\qbezier(30,40)(30,)(30,0) を変更 頂点から三角形を繋ぐ線を引くため $3/2=$4;f1 という制約条件を考える
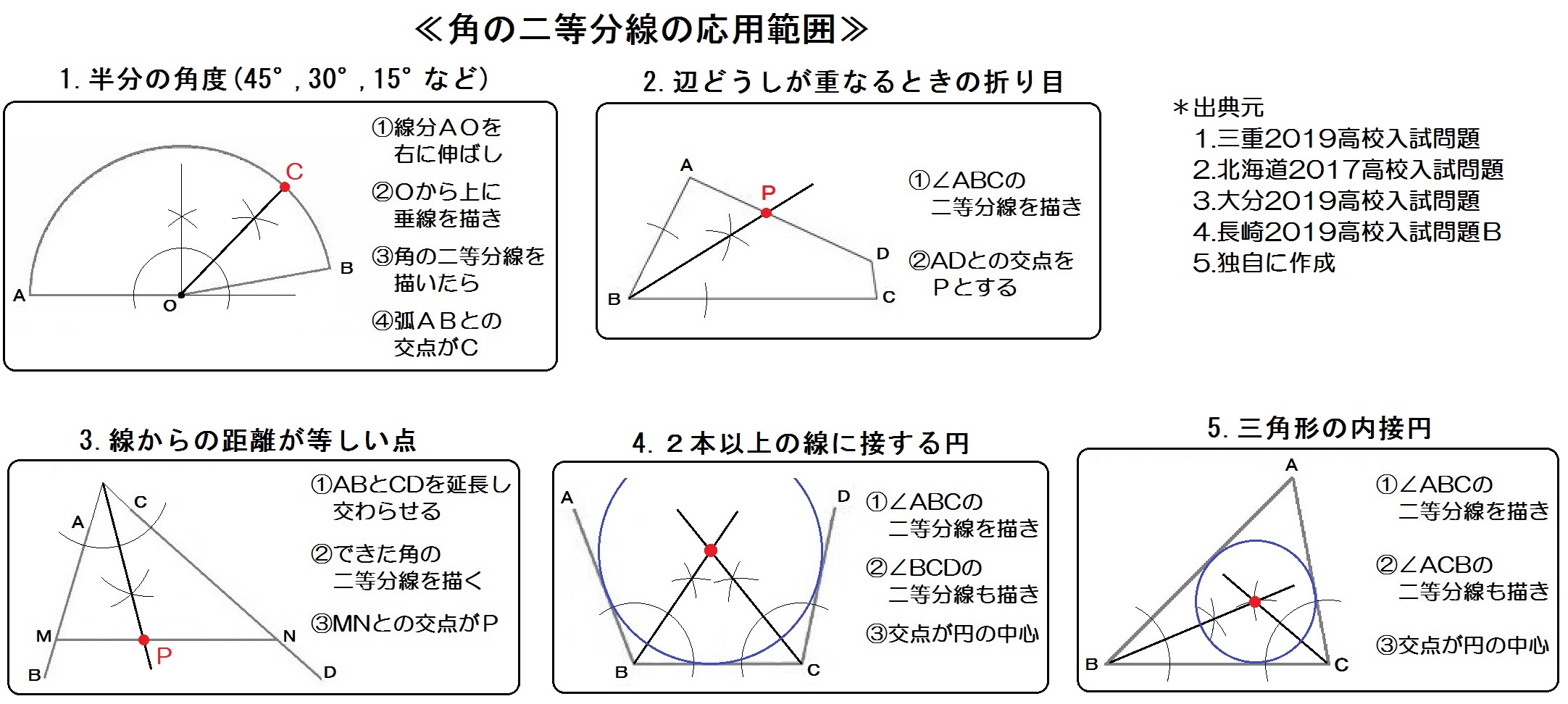
角の二等分線 の作図手順 コンパスの針を角の頂点Bに合わせ、それぞれの線分と交わるような弧を描く 交わった点を中心とした同じ半径の弧を描く 弧どうしが交わった点と角の頂点Bを結んだ線が角Bの二等分線となる三角形が二等辺三角形になるための条件につ いて統合的・発展的に考察し,論理的に確かめ表 現することができる. 2.本時の位置付け 本時は小単元「二等辺三角形」の第2時である. 第1時(前時)では,小学校で操作的に認めてこの場合正三角形の底辺に対する垂線の長さがRである。 よって2:√3=X:R → X=(2R・√3)/ Trek
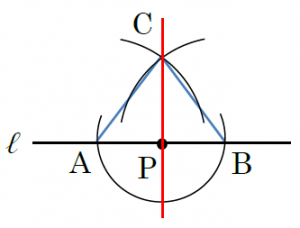
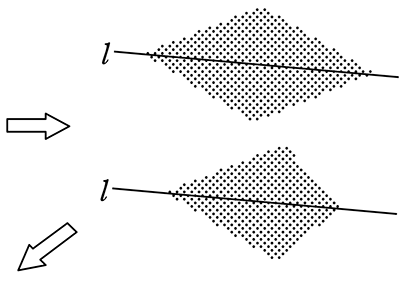
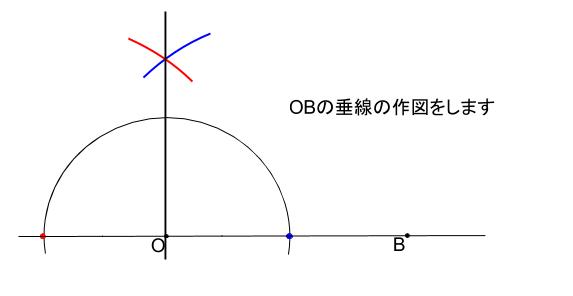
円に内接する正三角形の作図方法とは? 三角形の内接円・外接円の書き方を解説! 直角を三等分する線の作図方法とは 回転移動の中心を求める方法とは?作図の方法を解説! 最短距離にするためにはどこを通る?? 平行四辺形の書き方、コンパスを使っ中学数学の作図 作図のお約束事 中学数学で求められる作図とはある「作法」に則って進められます。 その「作法」とは、ゲームのルールのようなものです。 作図をするときの約束事 定規とコンパスだけを使う(もちろん鉛筆も使ってね 直線上の1点を通る垂線の作図 点C(直線上にある)を中心とする円をかき、直線ABとの交点をそれぞれP、Qとします 線分PQの両端の点を、それぞれ中心にして等しい半径の円をかき、交点をRとします 直線CRをひきましょう よく見てみると ②③は 「垂直




どうやって1本の直定規だけで30度の角度が作れます どうやって1本の直 教えて Goo




三角形の内接円の作図法と証明について 三角形の内接円の作図法と証明 数学 教えて Goo
三角形の相似条件 相似の問題の中でも、三角形の相似を証明する問題が多く出題されます。 ここでは、三角形の相似を証明するために必要な3つの条件を説明します。 私が実際に問題を解いた時に使う回数が多いと感じた順に書いてみました。 1つめは正三角形の高さの求め方、辺の長さの比は下記も参考になります。 正三角形の高さの求め方は?1分でわかる計算、面積の求め方、二等辺三角形の高さの求め方 正三角形の辺の比率は?1分でわかる値と計算方法、底辺と高さの比 まとめ三角グラフとは 三角グラフは、3つの辺に対応させた要素を項目として、それらの項目の比率を正三角形内部の点から各辺への垂線の長さで表したグラフです。 書き方と読み方(見方) 正三角形の性質ですが、正三角形内部のある点から各辺への垂直に
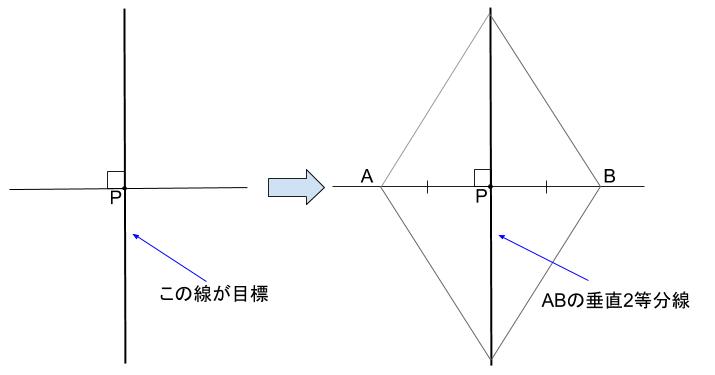



中学数学 垂線の作図 重要な2つ 中学数学の無料オンライン学習サイトchu Su



Studydoctor角の二等分線の作図と利用 中学1年数学 Studydoctor
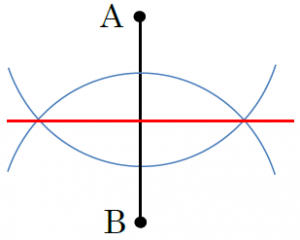
三辺の長さが与えられた三角形 解説 ※ 三辺の長さが与えられたときの三角形の高さや面積を求める問題は、高校の三角比の所で習います ので中学生でできなくても大丈夫です。 中学校では発展学習として掲載されている教科書があります。 (1 次の手順にて作図すると、希望の三角形ができます。 1)点Aおよび点Bを中心に半円を書きます。 2)半円の半径は線分ABの長さより幾分長いいものとします。 3)半円は点Aおよび点Bを中心に向かい合わせに書きます。やさしい星の書き方として、正五角形のほかに、正六角形、正八角形の書き方の一例をご紹介しましょう。 星形(正六角形)の書き方 (正6角形の作図) (1) 円を書きます。 (2) コンパスの幅はそのままで、円周上に印しを付けて行きます。




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく



中1数学 垂直な線の作図のしかた まなビタミン
正三角形と二等辺三角形 0700 ・どんぐり倶楽部の「良質の算数文章問題」にレイ君が取り組んでいます。 平日はママが、週末はパパが読み聞かせ、週2問のペースでやっています。 8/28、29実施 わからん帳行き 定規とコンパスを使って次の三角形の内心 ・ 外心 ・ 重心 三角形の3つの内角の2等分線は、1点で交わり、その点から3辺までの距離は等しい。 この1点で交わった点 I を三角形の内心という。 半径 IL の円が三角形の内接円である。三角形の面積(3辺からヘロンの公式) 4*sqrt (2) と入力してください。 sqrt関数をご使用ください。 たまに、的外れな指摘がありますが、この計算はまったく正しいです。 安心して使ってください。 ヘロンの公式を思い出し手計算を行いこのサイトで




中2の数学の直角三角形の証明なのですが Clear



この図で 頂点aから辺bcへの垂線はどうやって作図すれば良いのですか 作図 Yahoo 知恵袋
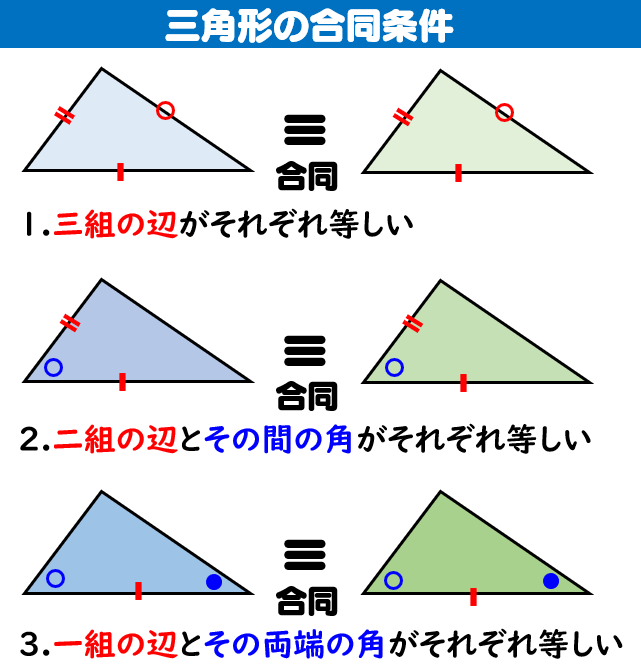
Q三角形の角度と距離の関係で 基点からある角度で上昇した場合、ある点で垂線を下ろした時の、 基点までの距離を知りたいのですが法則みたいな物は有るのでしょうか? 理系に疎いもので分かりづらいと思いますが・・・ たとえば角度15度の斜辺で30cm上昇地点で垂線をおろした点の 小5算数「合同な図形」の問題 どこよりも簡単な解き方・求め方 2つの図形の形と大きさが全く同じとき「2つの図形は合同である」と言います 合同な図形の対応する辺、角は等しいです 合同な三角形の書き方は中学校の数学でも大切な考え方になるので、しっかり確認しておきま




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく




作図 三角形の高さをコンパスを使ってかく問題を解説 Youtube



コンパスと定規を使った垂直線の描き方 図形の描き方001a 夏貸文庫




三角形の垂心と重心 数学a By Okボーイ マナペディア




垂線の書き方 作図 中学1年数学 Youtube




垂線の作図 手順と なぜ について解説します 中学数学 理科の学習まとめサイト



正三角形の書き方 高さが6センチの正三角形を描きたいです どのように描けば Yahoo 知恵袋



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ



中1数学 垂直な線の作図のしかた まなビタミン



コンパスと定規を使った垂直線の描き方 図形の描き方001a 夏貸文庫




角の二等分線の作図 Youtube




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく




作図ー垂線 いろいろな問題 無料で使える中学学習プリント



中学数学 作図 円と接線 接点 中学数学の無料オンライン学習サイトchu Su



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ



中1数学 垂直な線の作図のしかた まなビタミン



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ




簡単にわかる 垂線を作図する方法 苦手な数学を簡単に




懐かしの数学作図 直線上の点pを通る垂線を引く の作図問題を コンパスを1回だけ使って 解く 圧倒亭グランパのブログ
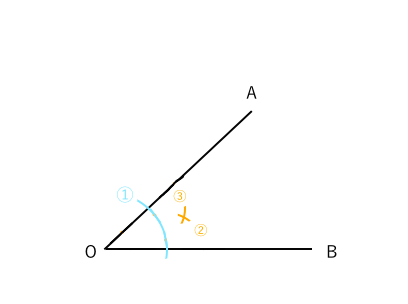



簡単にわかる 角の二等分線を作図する方法 苦手な数学を簡単に



三角定規のおすすめ人気ランキング15選 平行線や垂線を使った作図 製図に セットや可愛いものも Best One ベストワン




作図の3種類 垂直二等分線 角の二等分線 垂線 は 実は同じ図形だ 東大に文理両方で合格した男が綴る 受験の戦略




数学 三角形の内心とは 角の二等分線の作図を踏まえた内接円の書き方と証明 Curlpingの幸せblog



垂線 の2通りの作図方法 コンパス 定規 数学fun




証明の書き方で最初に と において と書く時 Clearnote




中1数学 垂直二等分線の作図 練習編 映像授業のtry It トライイット




応用 90度に関連する作図 なかけんの数学ノート



雑学のソムリエ 平行線の作図



Mathematics 作図 1 作図の基本問題 働きアリ
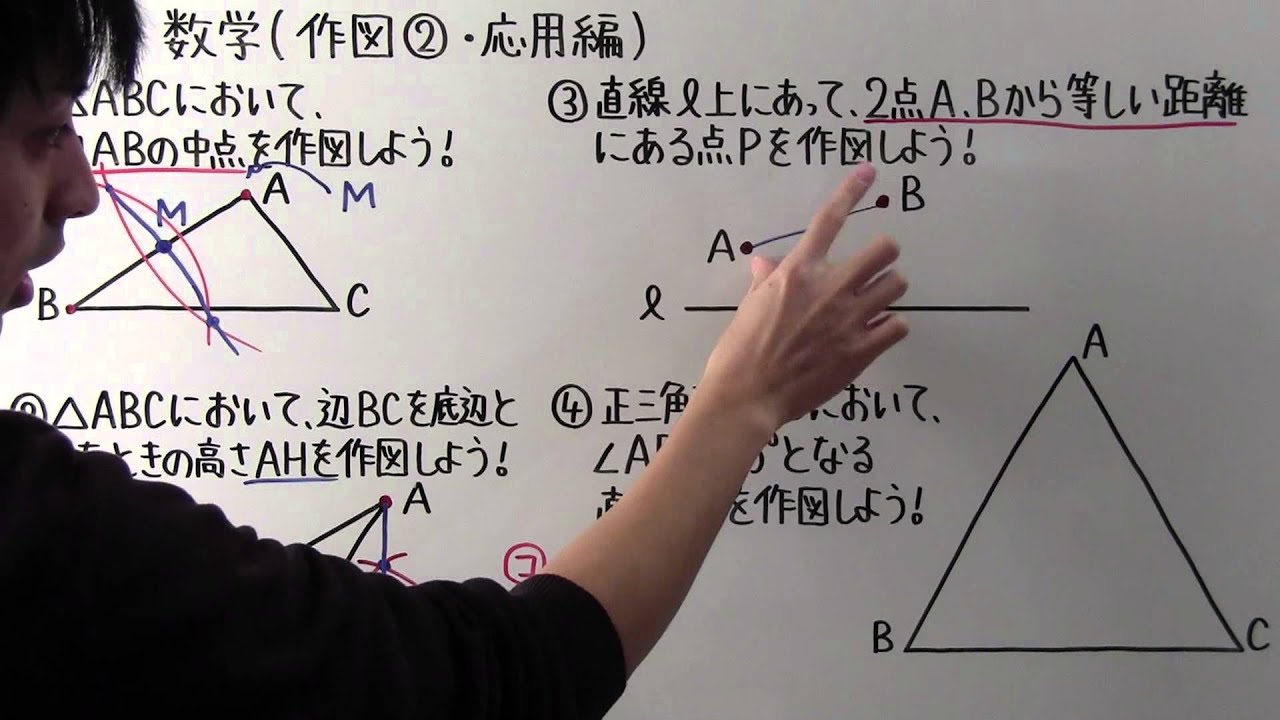



中1 数学 中1 70 作図 応用編 Youtube




標準 75度や150度の作図 なかけんの数学ノート



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ
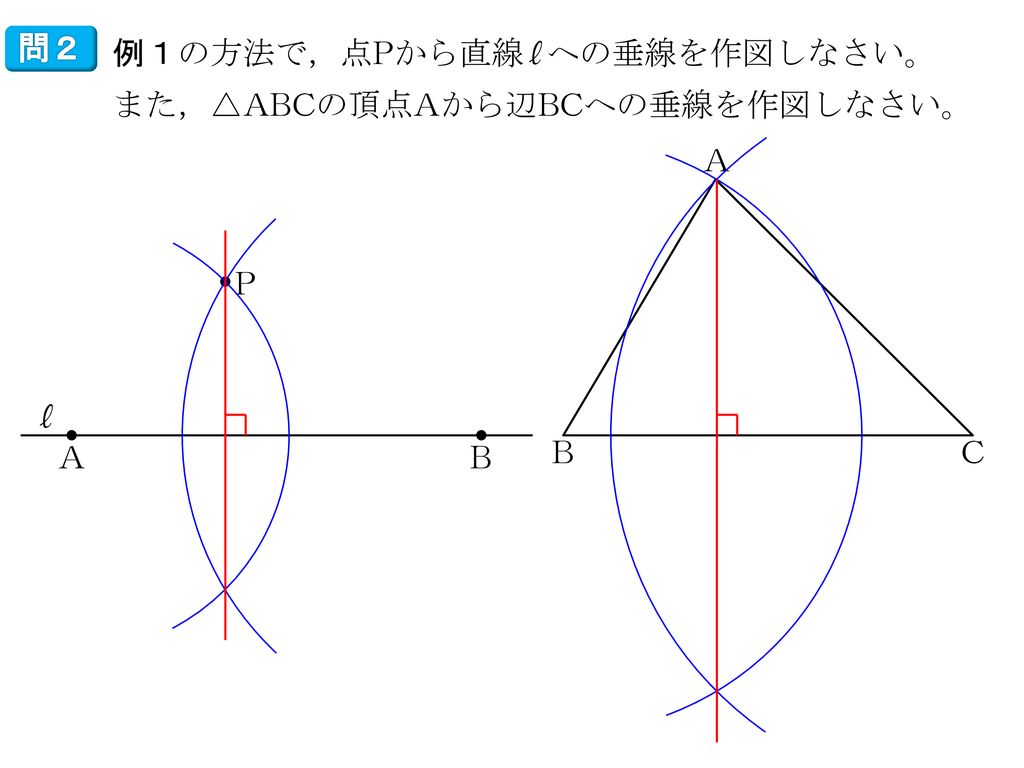



中学数学1年 5章 平面図形 2 作図 3時間 Ppt Download



内接円 内心




コンパス作図 45度の角度の出し方を解説するよ 中学数学 理科の学習まとめサイト



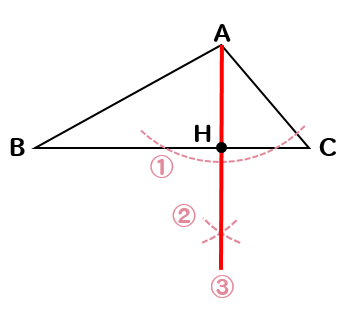
垂線の作図方法を教えて下さい 三角形abcで点aを通る直線bcの垂線の作 Yahoo 知恵袋




垂直二等分線の作図方法 書き方 と なぜ正しいのか 証明をわかりやすく解説 垂線 遊ぶ数学



3
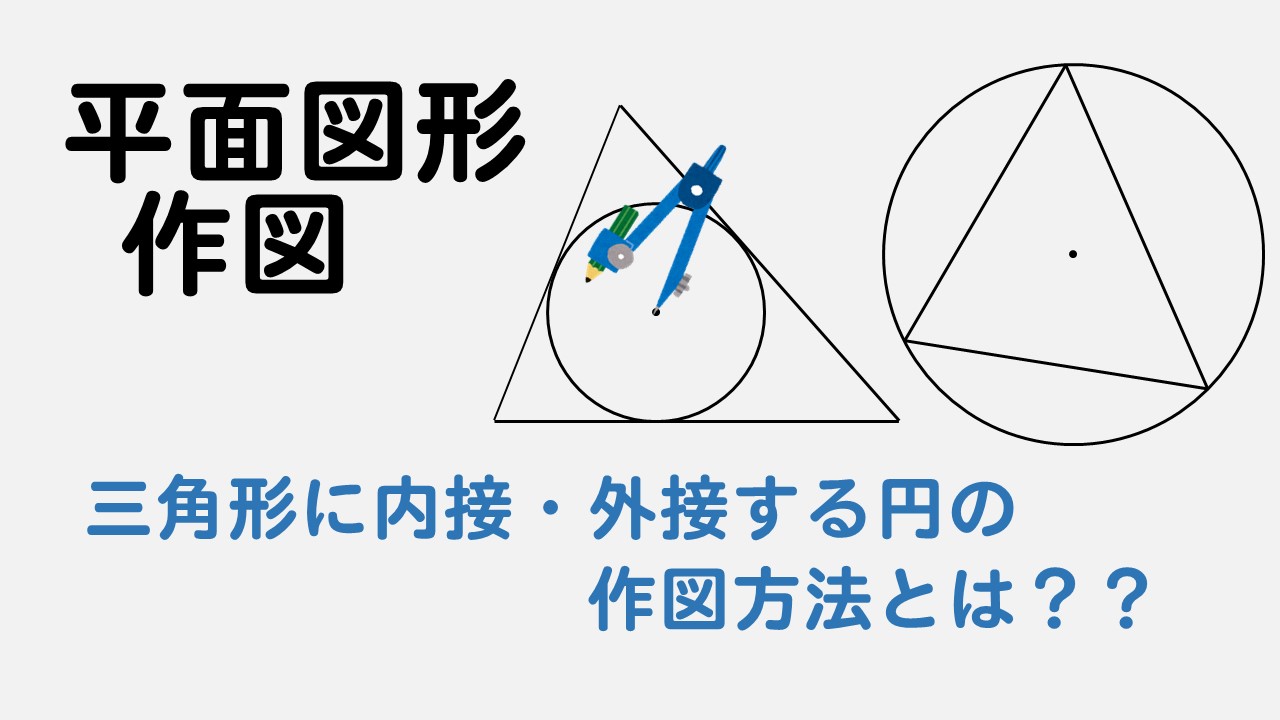



作図 三角形の内接円 外接円のかき方をポイント解説 数スタ



垂心について



中1数学 垂直な線の作図のしかた まなビタミン




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ



三角形に接する円 中学から数学だいすき




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく



Math 円と作図 外接円 内接円 外心 内心 重心 垂心と作図 働きアリ



作図の証明 中学から数学だいすき




三角形の内心について知っておきたい知識まとめ 理系ラボ




Aを頂点のひとつと Bがpqの中点になる正三角形apqの作図の問題です Clearnote
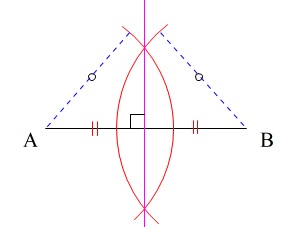



作図問題の解き方と入試問題 角の二等分線 垂線 円の接線他



Http Www Hyogo C Ed Jp Gimu Bo Gakuryokutyousa Kadai H28 07 28a41 Pdf




標準 折り目の作図 なかけんの数学ノート
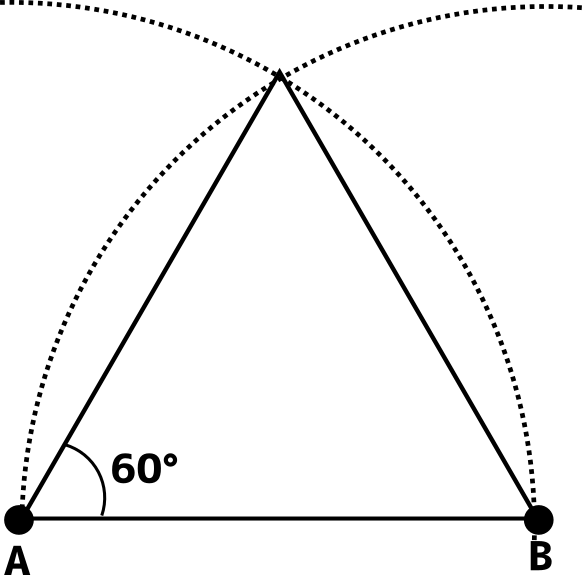



30 45 60 の作図 チーム エン
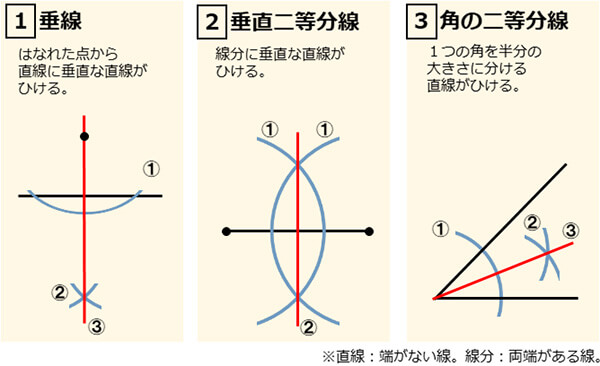



数学の 作図問題 が苦手 得点源にするコツ教えます 高校入試よくでる 2 ベネッセ教育情報サイト



1




二等辺三角形の面積をどうやって求めるの 考え方のコツは三角定規に着目すること 中学受験ナビ



三角形の面積を二等分する 垂線 理系男子の独り善がり



1
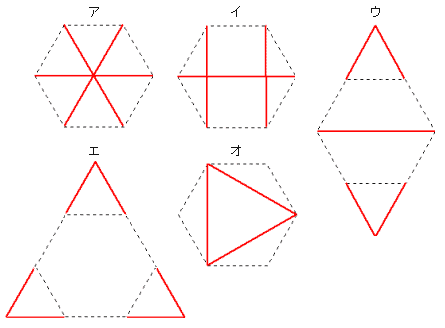



課題学習の指導 数学



作図 三角形の高さをコンパスを使ってかく問題を解説 数スタ




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく




正三角形 の作図方法 コンパス 定規 数学fun



1




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく




垂直 平行な線の書き方 Youtube



中学数学 平面図形



中学数学 平面図形 のコツ 角の二等分線 垂線を使った作図




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく



垂線の作図の証明




証明問題です 書き方がわからないです これで合ってますかね Clearnote
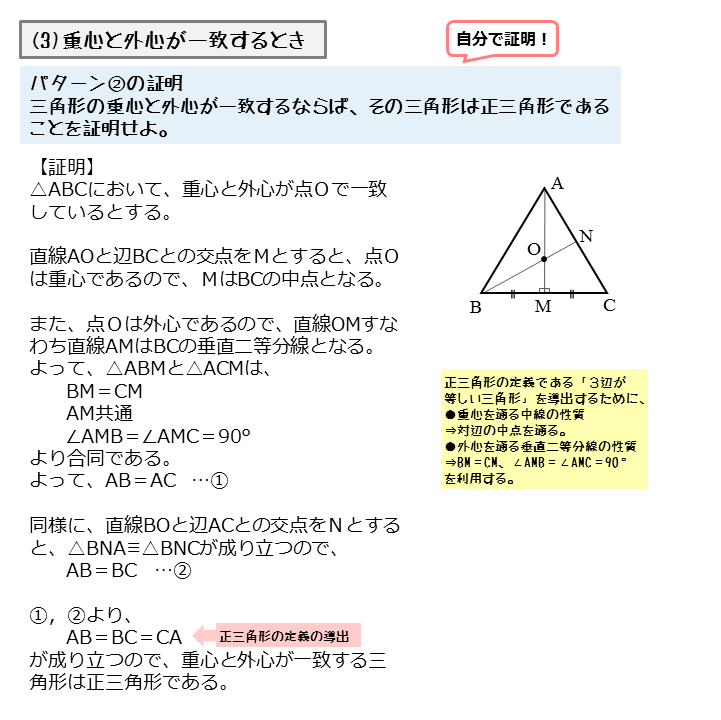



図形の性質 正三角形の外心 内心 重心について 日々是鍛錬 ひびこれたんれん
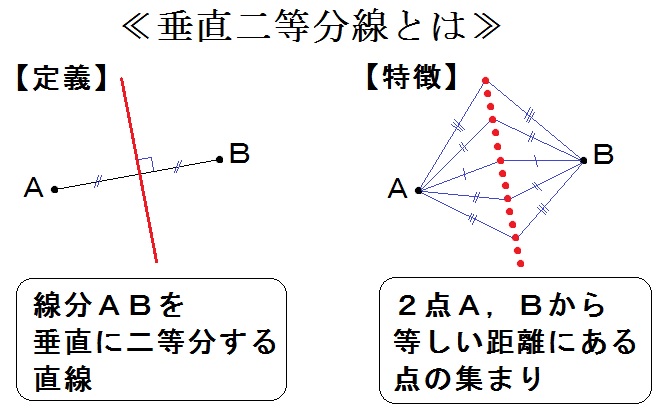



中学数学 平面図形 のコツ 垂直二等分線を使った作図
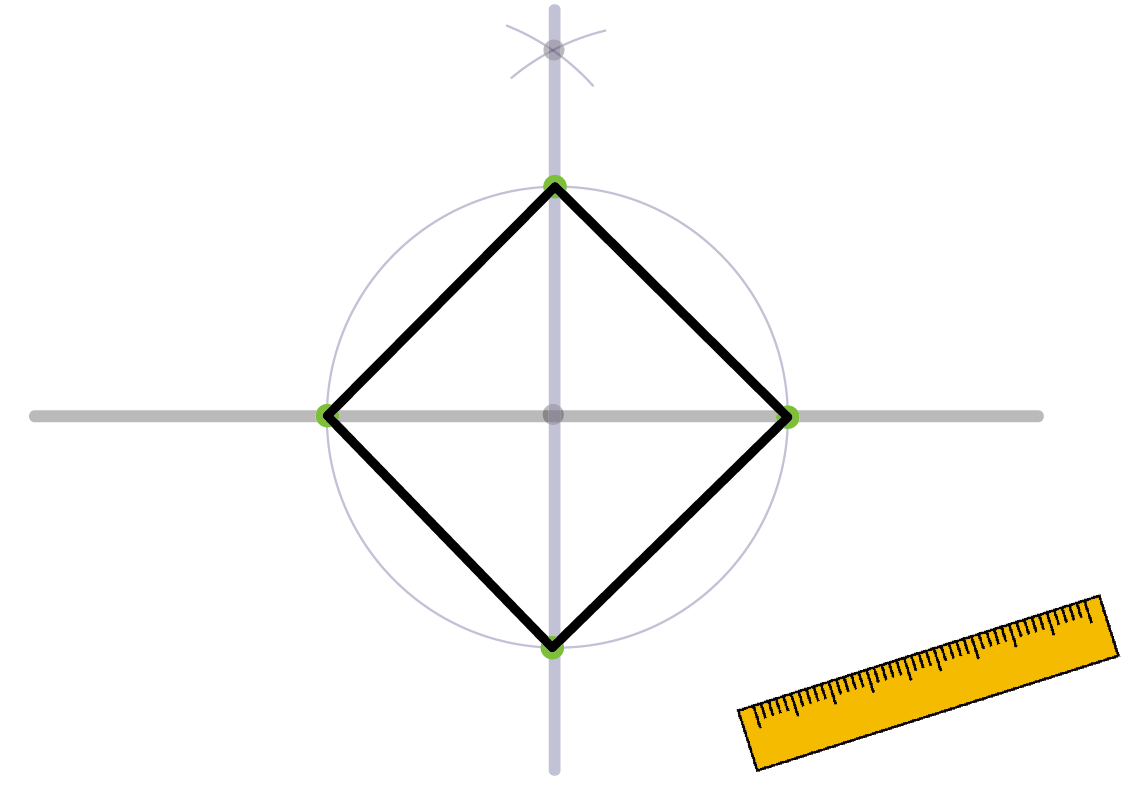



コンパスで作図 正方形の書き方がわかる5つのステップ Qikeru 学びを楽しくわかりやすく
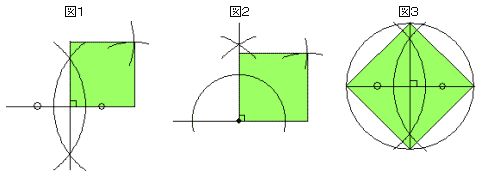



課題学習の指導 数学
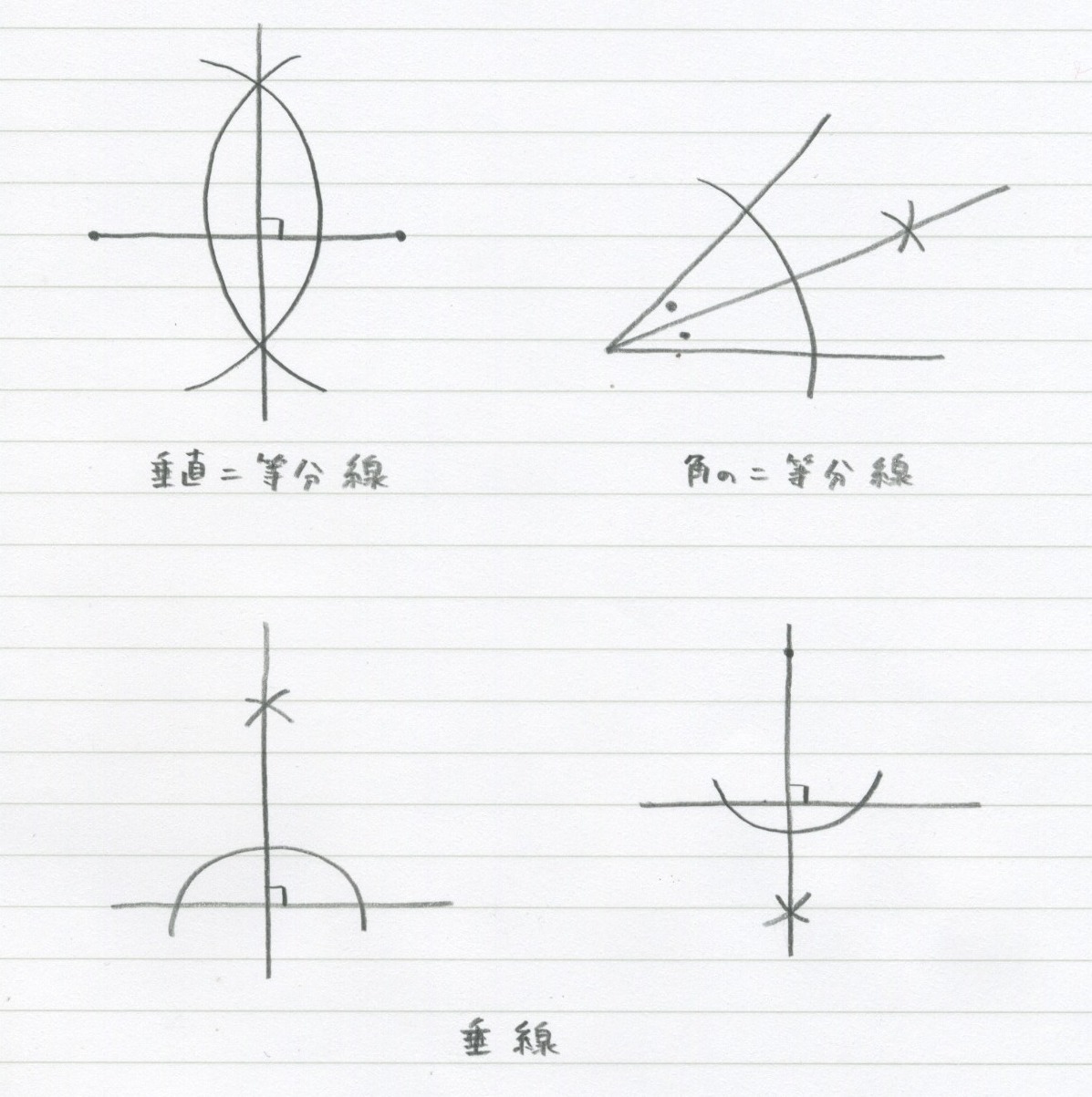



12 1 作図 結局4つ 勉強できようサイト
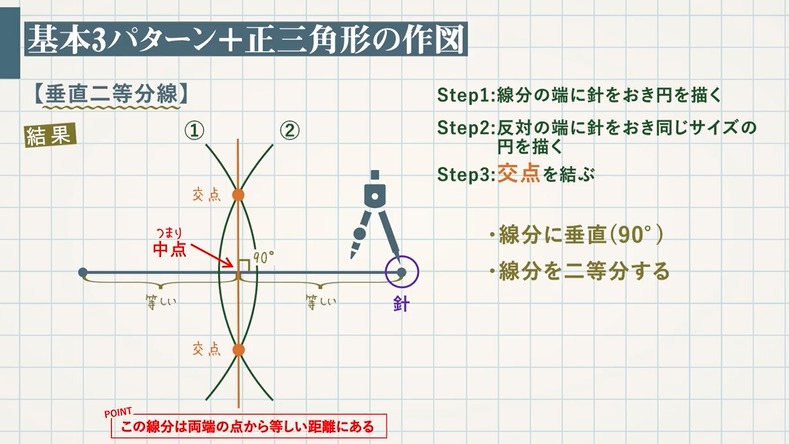



1年生で習う作図まとめ 教遊者



三角形の五心 重心 内心 外心 垂心 傍心 の作図方法まとめ 受験辞典
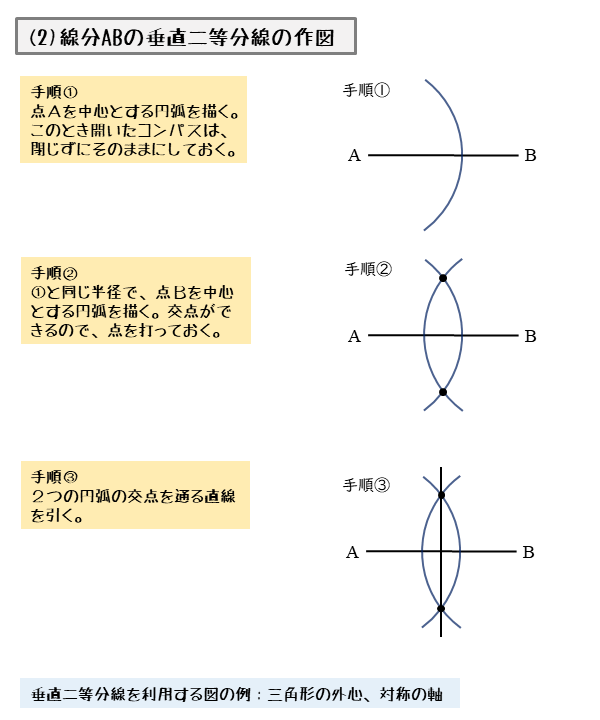



図形の性質 作図について 日々是鍛錬 ひびこれたんれん
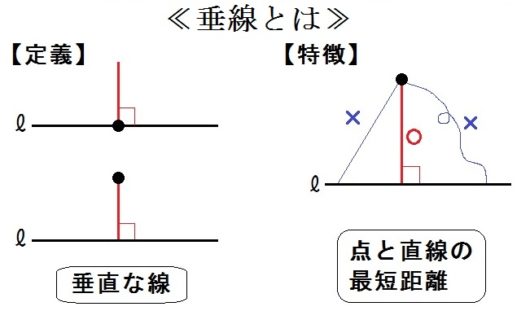



中学数学 平面図形 のコツ 作図の高校入試問題を解いてみよう




基本の作図について 承前 中学数学教材研究ノート




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく



垂線の応用 三角形の高さの作図 デジタル教科書 電子教科書




中1数学 5ステップでわかる 垂線の作図 書き方 Qikeru 学びを楽しくわかりやすく
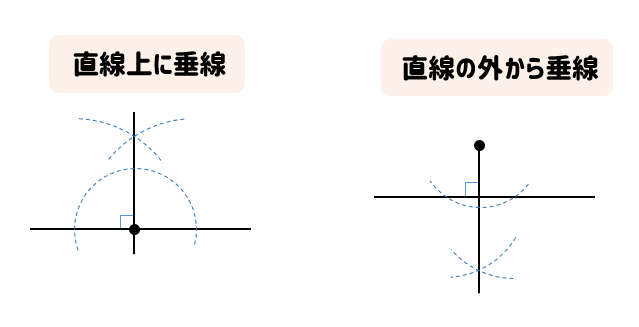



作図 垂線のやり方は 使える問題をパターン別に確認しておこう 数スタ



正三角形とは 定義や面積公式 高さや角度の求め方 受験辞典



中学数学 作図 30 45 有名角の作図 中学数学の無料オンライン学習サイトchu Su




垂線の作図 Youtube
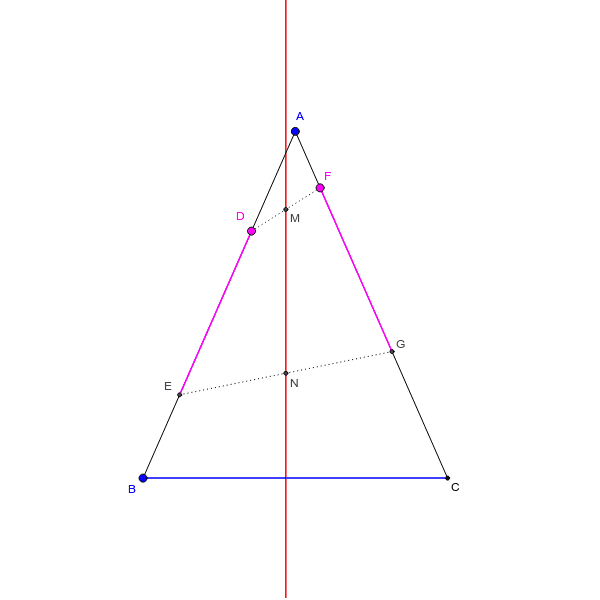



二等辺三角形と垂線 Geogebra
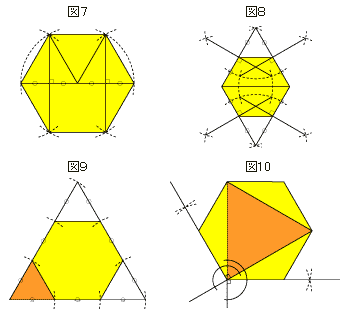



課題学習の指導 数学
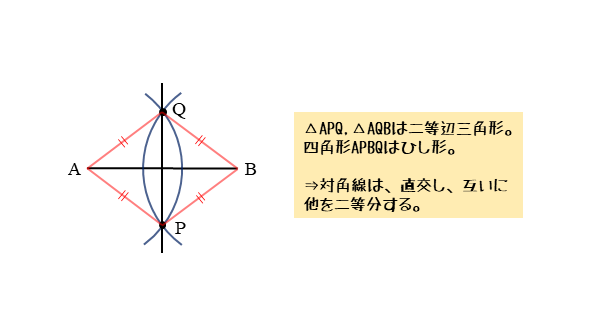



図形の性質 作図について 日々是鍛錬 ひびこれたんれん




テストでこんな問題が出ました Clear




直角三角形の合同条件を使った証明とは なぜ2つ増えるのか 遊ぶ数学




標準 平行移動に関する作図 なかけんの数学ノート



中1です 三角形abcの垂心の書き方を教えてください Bの垂線は引 Yahoo 知恵袋




三角形の垂心について知っておきたい知識まとめ 理系ラボ


